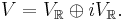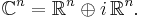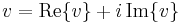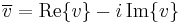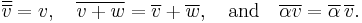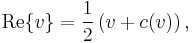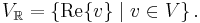Reality structure
In mathematics, a reality structure on a complex vector space V is a decomposition of V into two real subspaces, called the real and imaginary parts of V:
Here VR is a real subspace of V, i.e. a subspace of V considered as a vector space over the real numbers. If V has complex dimension n (real dimension 2n), then VR must have real dimension n.
The standard reality structure on the vector space 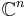 is the decomposition
is the decomposition
In the presence of a reality structure, every vector in V has a real part and an imaginary part, each of which is a vector in VR:
In this case, the complex conjugate of a vector v is defined as follows:
This map 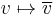 is an antilinear involution, i.e.
is an antilinear involution, i.e.
Conversely, given an antilinear involution 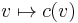 on a complex vector space V, it is possible to define a reality structure on V as follows. Let
on a complex vector space V, it is possible to define a reality structure on V as follows. Let
and define
Then
This is actually the decomposition of V as the eigenspaces of the real linear operator c. The eigenvalues of c are +1 and −1, with eigenspaces VR and  VR, respectively. Typically, the operator c itself, rather than the eigenspace decomposition it entails, is referred to as the reality structure on V.
VR, respectively. Typically, the operator c itself, rather than the eigenspace decomposition it entails, is referred to as the reality structure on V.
See also
References
- Penrose, Roger; Rindler, Wolfgang (1986), Spinors and space-time. Vol. 2, Cambridge Monographs on Mathematical Physics, Cambridge University Press, ISBN 978-0-521-25267-6, MR838301